Page 270 - 360.revista de Alta Velocidad - Nº 5

Álvarez, Fernando. Balmaseda, Lucía. Gallego, Inmaculada. Rivas , Ana. Sánchez-Cambronero, San

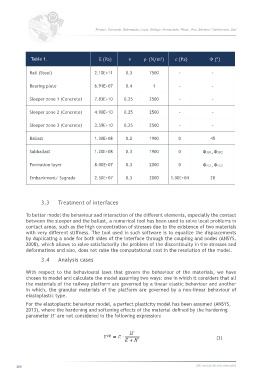
Table 1. E (Pa) v ρ (N/m ) c (Pa) Φ (°)
3

Rail (Steel) 2.10E+11 0.3 7500 - -

Bearing plate 6.91E+07 0.4 1 - -

Sleeper zone 1 (Concrete) 7.83E+10 0.25 2500 - -

Sleeper zone 2 (Concrete) 4.90E+10 0.25 2500 - -

Sleeper zone 3 (Concrete) 3.59E+10 0.25 2500 - -

Ballast 1.30E+08 0.2 1900 0 45

Subballast 1.20E+08 0.3 1900 0 Φ1, Φ2

Formation layer 8.00E+07 0.3 2000 0 Φ1, Φ2

Embankment/ Sugrade 2.50E+07 0.3 2000 1.00E+04 20

3.3 Treatment of interfaces

To better model the behaviour and interaction of the different elements, especially the contact
between the sleeper and the ballast, a numerical tool has been used to solve local problems in
contact areas, such as the high concentration of stresses due to the existence of two materials
with very different stiffness. The tool used in such software is to equalize the displacements
by duplicating a node for both sides of the interface through the coupling and nodes (ANSYS,
2008), which allows to solve satisfactorily the problem of the discontinuity in the stresses and
deformations and also, does not raise the computational cost in the resolution of the model.

3.4 Analysis cases

With respect to the behavioural laws that govern the behaviour of the materials, we have
chosen to model and calculate the model assuming two ways: one in which it considers that all
the materials of the railway platform are governed by a linear elastic behaviour and another
in which, the granular materials of the platform are governed by a non-linear behaviour of
elastoplastic type.
For the elastoplastic behaviour model, a perfect plasticity model has been assumed (ANSYS,
2013), where the hardening and softening effects of the material defined by the hardening
parameter ´ are not considered in the following expression:

268 360.revista de alta velocidad