Page 317 - 360.revista de Alta Velocidad - Nº 6

Regional diffusion and adoption effects on HSR demand expansion

The Bass model can also be interpreted by a hazard rate. The interpretation of the hazard is
that if it is multiplied by a small time increment it gives the probability that a random pur-
chaser who has not yet made the purchase will do so in the next small time increment (Wang,
2012). The hazard rate indicates “the portion that adopts at t given that they have not yet
adopted”, thus this formula can be written as follows:

The probability of adopting by those who have not yet adopted is regarded as a linear function
of those who have previously adopted it, i.e.

Where h(t) means the conditional likelihood that HSR users will adopt the innovation at exactly
time t since introduction, given that the users has not adopted before that time ft is the
likelihood for any randomly selected individual to adopt at time t (Rate at which the probability
of adoption is changing at time t), and F(t) is the market saturation at time t (Probability
density function of adoption at time t). Yt is the accumulated number of customers who have
already adopted the innovation by time t and N is a parameter representing the total number
of HSR users in the adopting target segment, all of whom will eventually adopt HSR. p is the
“innovation coefficient”’ and q is the “imitation coefficient”. Bass (1969) calibrated the curve
and parameters p and q for a range of products ranging from lawn moreover to microwaves.
We hypothesize that we can use the product adoption model also to improve estimates regarding
HSR demand uptake. It is important to note that our interpretation of p and q changes.
Originally in the model, the interpretation of these coefficientscan be directly associated with
“innovators” and “imitators”. In the case of HSR travel though it is not a “single purchase”
we are interested in but the general increase in using HSR. We therefore re-interpret p as
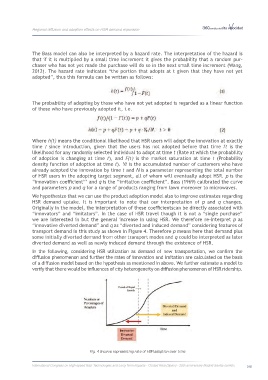
“innovative diverted demand” and q as “diverted and induced demand” considering features of
transport demand in this study as shown in Figure 4. Therefore p means here that demand plus
some initially diverted demand from other transport modes and q could be interpreted as later
diverted demand as well as newly induced demand through the existence of HSR.
In the following, considering HSR utilization as demand of new transportation, we confirm the
diffusion phenomenon and further the rates of innovation and imitation are calculated on the basis
of a diffusion model based on the hypothesis as mentioned in above. We further estimate a model to
verify that there would be influences of city heterogeneity on diffusion phenomenon of HSR ridership.

Fig. 4 S-curve representing rate of HSR adoption over time

International Congress on High-speed Rail: Technologies and Long Term Impacts - Ciudad Real (Spain) - 25th anniversary Madrid-Sevilla corridor 315