Page 277 - 360.revista de Alta Velocidad - Nº 5

Calculation and rational dimensioning of railway infrastructure materials using numerical modelling

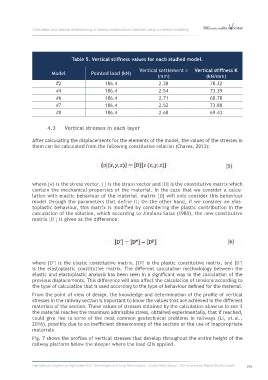
Table 5. Vertical stiffness values for each studied model.

Vertical settlement Vertical stiffness K
Model Pointed load (kN)
(mm) (kN/mm)
#2 186.4 2.38 78.32
#4 186.4 2.54 73.39
#6 186.4 2.71 68.78
#7 186.4 2.52 73.88
#8 186.4 2.68 69.43

4.3 Vertical stresses in each layer

After calculating the displacements for the elements of the model, the values of the stresses in
them can be calculated from the following constitutive relation (Chaves, 2013):

where {} is the stress vector, { } is the strain vector and [D] is the constitutive matrix which
contain the mechanical properties of the material. In the case that we consider a calcu-
lation with elastic behaviour of the material, matrix [D] will only consider this behaviour
model through the parameters that define it; On the other hand, if we consider an elas-
toplastic behaviour, this matrix is modified by considering the plastic contribution in the
calculation of the solution, which according to Jiménez Salas (1980), the new constitutive
matrix [D´] is given as the difference:

where [D ] is the elastic constitutive matrix, [D ] is the plastic constitutive matrix, and [D´]
p
e
is the elastoplastic constitutive matrix. The different calculation methodology between the
elastic and elastoplastic analysis has been seen in a significant way in the calculation of the
previous displacements. This difference will also affect the calculation of tensions according to
the type of calculation that is used according to the type of behaviour defined for the material.
From the point of view of design, the knowledge and determination of the profile of vertical
stresses in the railway section is important to know the values that are achieved in the different
materials of the section. These values of stresses obtained by the calculation allow us to see if
the material reaches the maximum admissible stress, obtained experimentally, that if reached,
could give rise to some of the most common geotechnical problems in railways (Li, et.al.,
2016), possibly due to an inefficient dimensioning of the section or the use of inappropriate
materials
Fig. 7 shows the profiles of vertical stresses that develop throughout the entire height of the
railway platform below the sleeper where the load Q is applied.

International Congress on High-speed Rail: Technologies and Long Term Impacts - Ciudad Real (Spain) - 25th anniversary Madrid-Sevilla corridor 275