Page 310 - 360.revista de Alta Velocidad - Nº 5

Balmaseda, Lucía. Gallego, Inmaculada. Sánchez-Cambronero, Santos. Rivas, Ana.

From Table 3, we note that the values obtained in sleeper T7 are always similar to the values
obtained for the two adjacent sleepers. Three loading conditions did not have to be consi-
dered; two conditions would have been sufficient. This finding is explained by the fact that
the largest plastic deformation is caused by the loads from the weight of the wheel; it is not
caused by the loads from the passage of an axle.

3. Comparison of the numerical model results with the results obtained with
the Eisenmann formula.

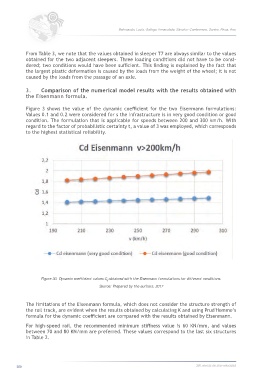
Figure 3 shows the value of the dynamic coefficient for the two Eisenmann formulations:
Values 0.1 and 0.2 were considered for s the infrastructure is in very good condition or good
condition. The formulation that is applicable for speeds between 200 and 300 km/h. With
regard to the factor of probabilistic certainty t, a value of 3 was employed, which corresponds
to the highest statistical reliability.

Figure 30. Dynamic coefficient values C obtained with the Eisenmann formulations for different conditions.
d
Source: Prepared by the authors, 2017

The limitations of the Eisenmann formula, which does not consider the structure strength of
the rail track, are evident when the results obtained by calculating K and using Prud'Homme’s
formula for the dynamic coefficient are compared with the results obtained by Eisenmann.

For high-speed rail, the recommended minimum stiffness value is 60 KN/mm, and values
between 70 and 80 KN/mm are preferred. These values correspond to the last six structures
in Table 2.

308 360.revista de alta velocidad